Projects

-- Relaxation Oscillation in Predator-Prey Systems

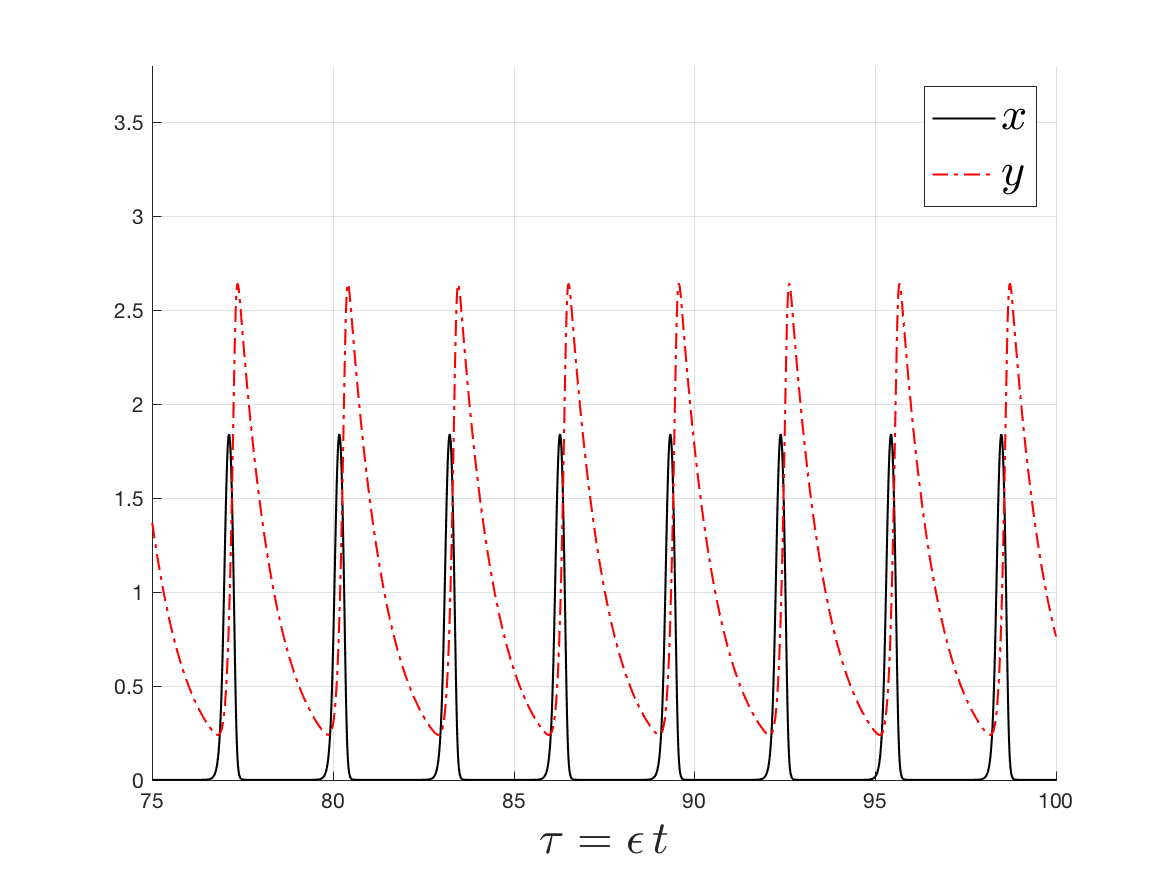
For the classical predator-prey systems with general functional response, I study the limiting behaviour of the periodic orbits as the predator death rates approach zero. Using the geometric singular perturbation theory and the theory of Floquet multipliers, I classified the number and stability of periodic orbits for a class of response functions according on their geometric properties. [arXiv]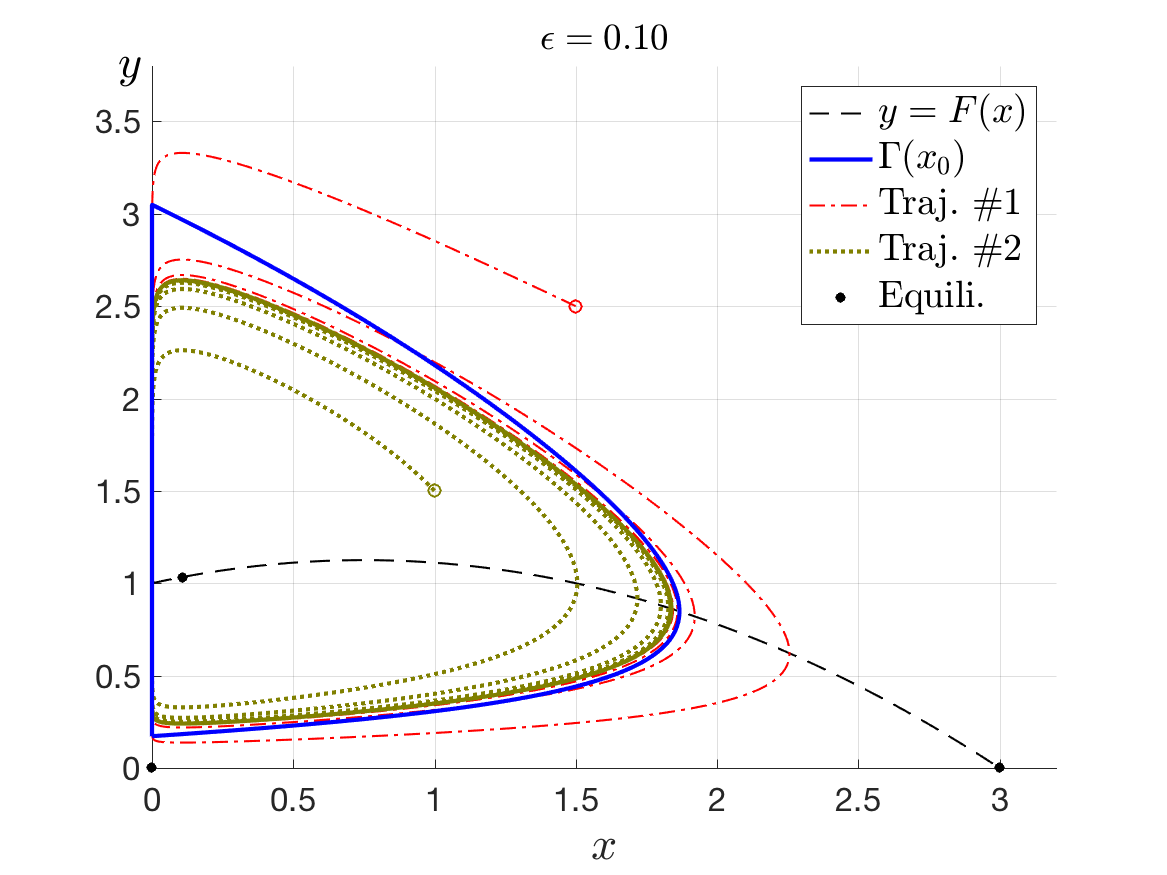

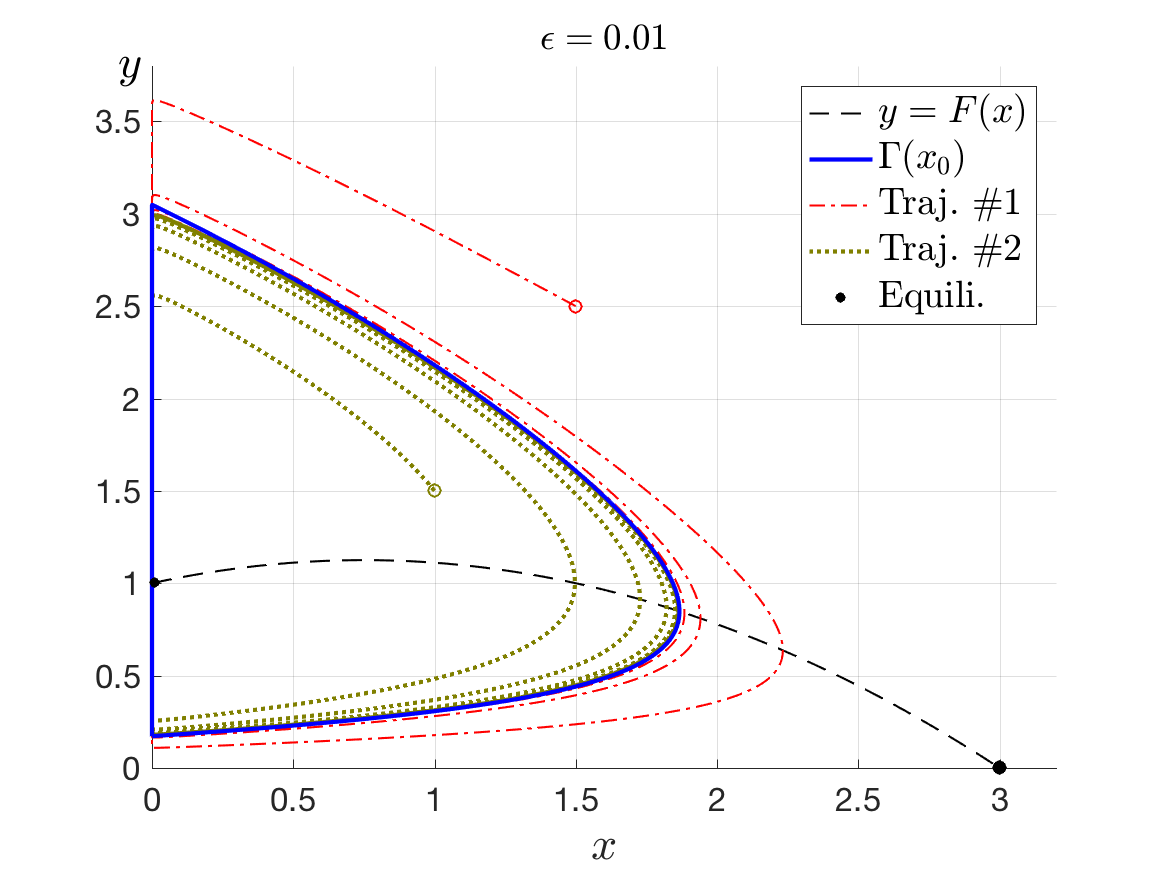
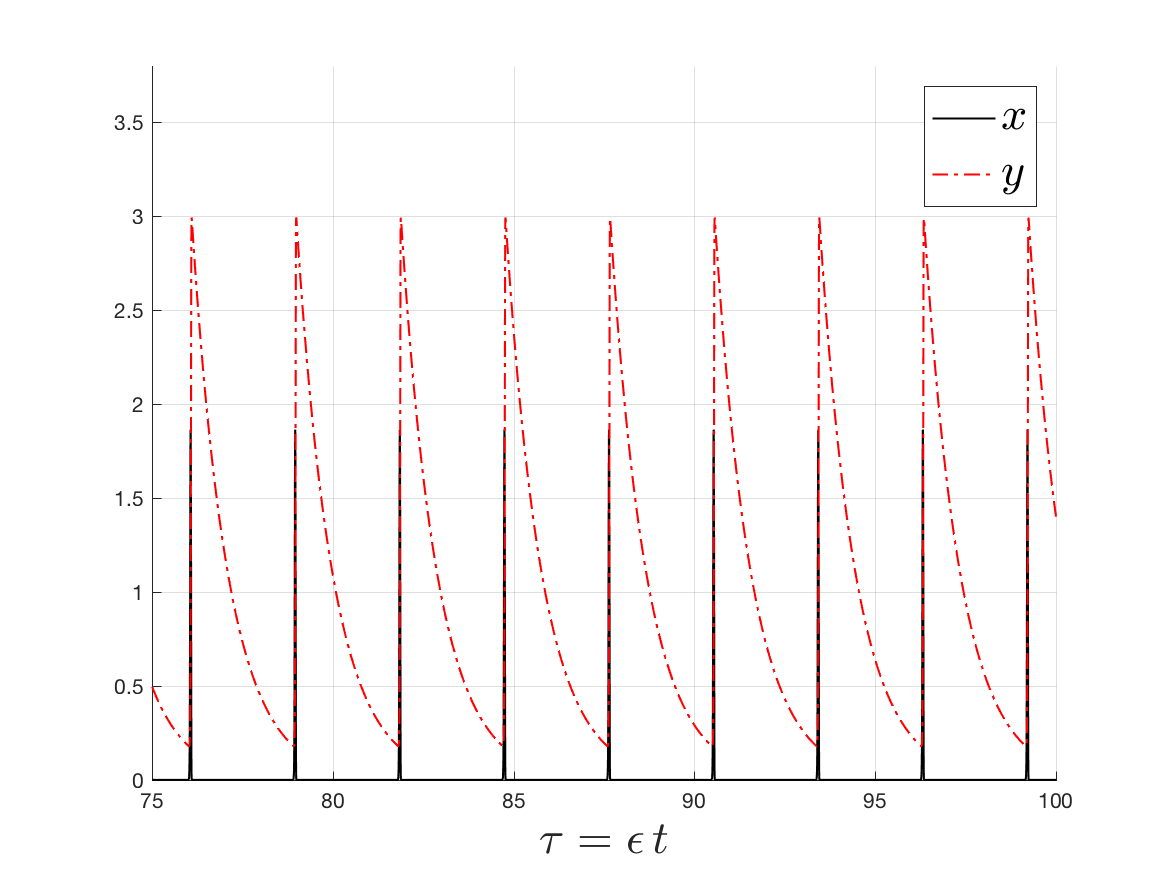
-- Advancing the Geometric Singular Perturbation Theory

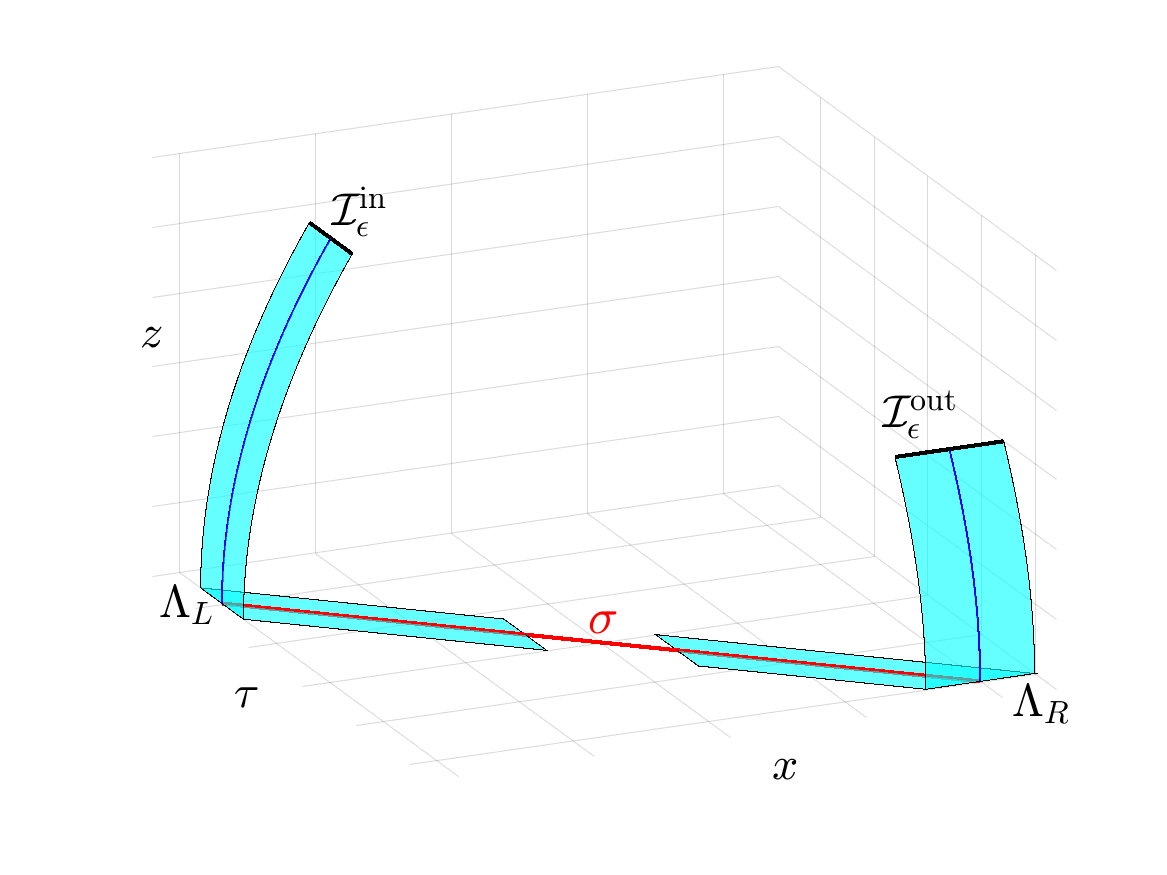
The phenomenon of bifurcation delay is that, for a certain class of slow-fast systems, the limiting attracting and repulsion points are given by the entry-exit relation. The phenomenon is has been proved using various methods in the literature. With a novel use of geometric singular perturbation theory, I implemented a new proof that provides new geometrical insights. [DOI]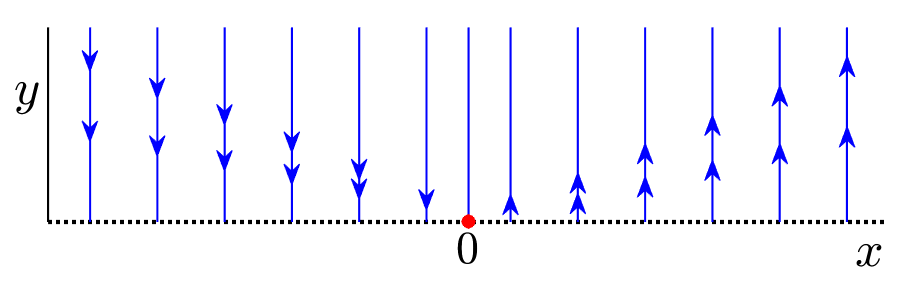

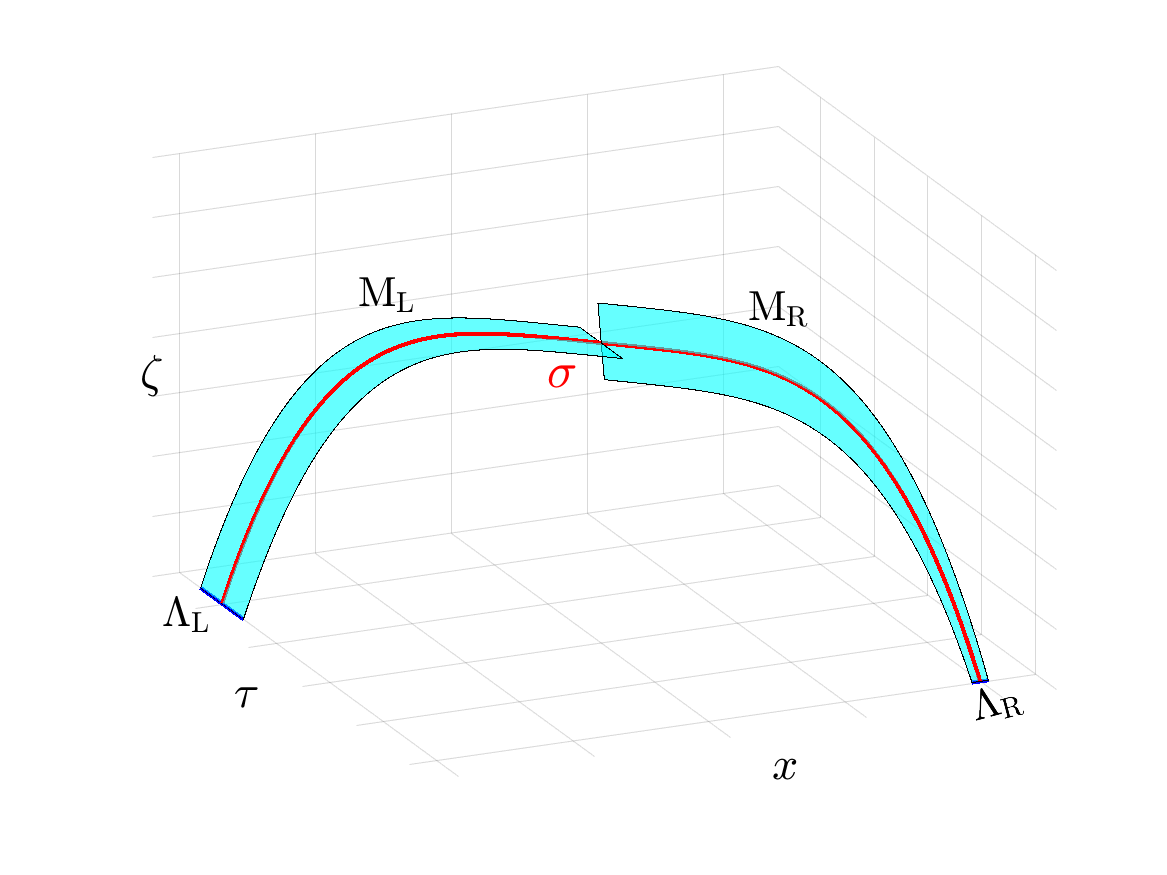
-- Singular Shocks in Nonlinear Conservation Laws

Besides regular shocks and rarefaction waves, singular shocks is another type of solutions for Riemann problems for systems of conservation laws. My Ph.D. thesis focused on viscous profile for singular shocks. [DOI]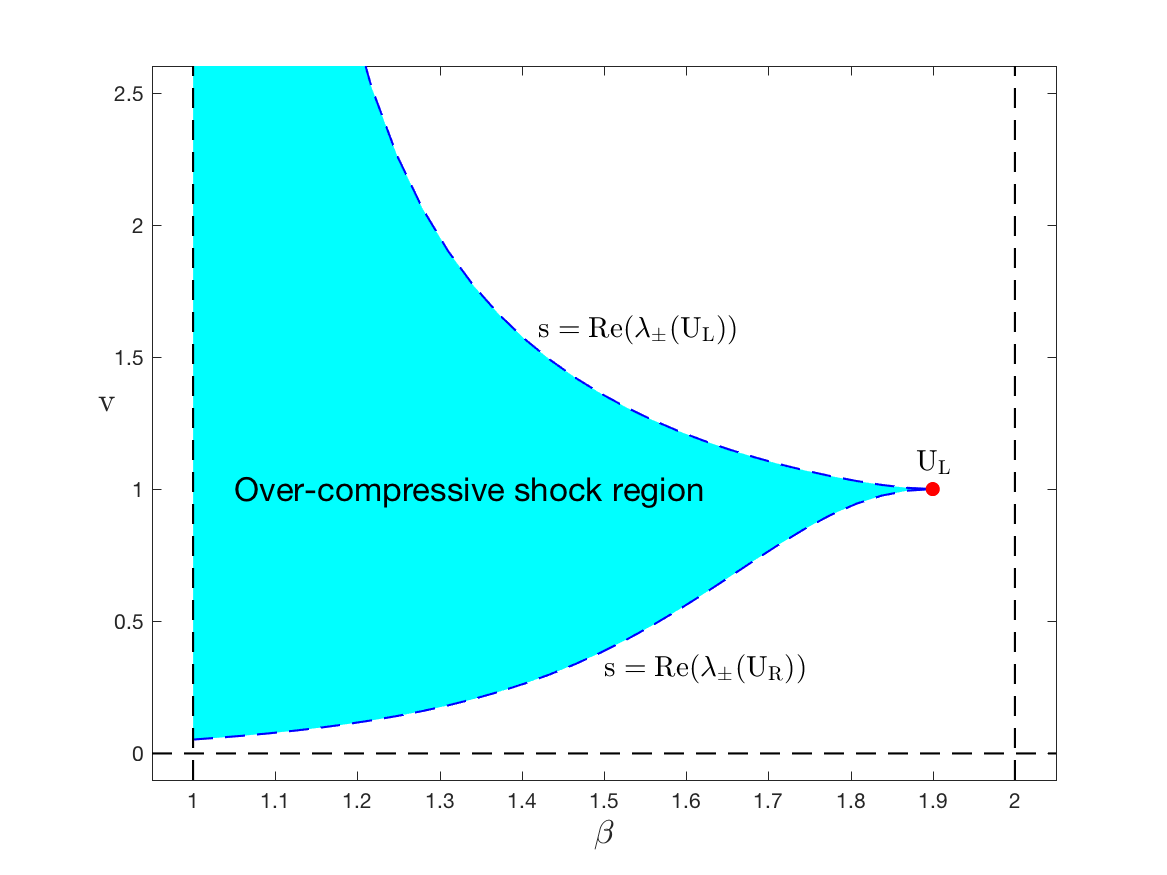

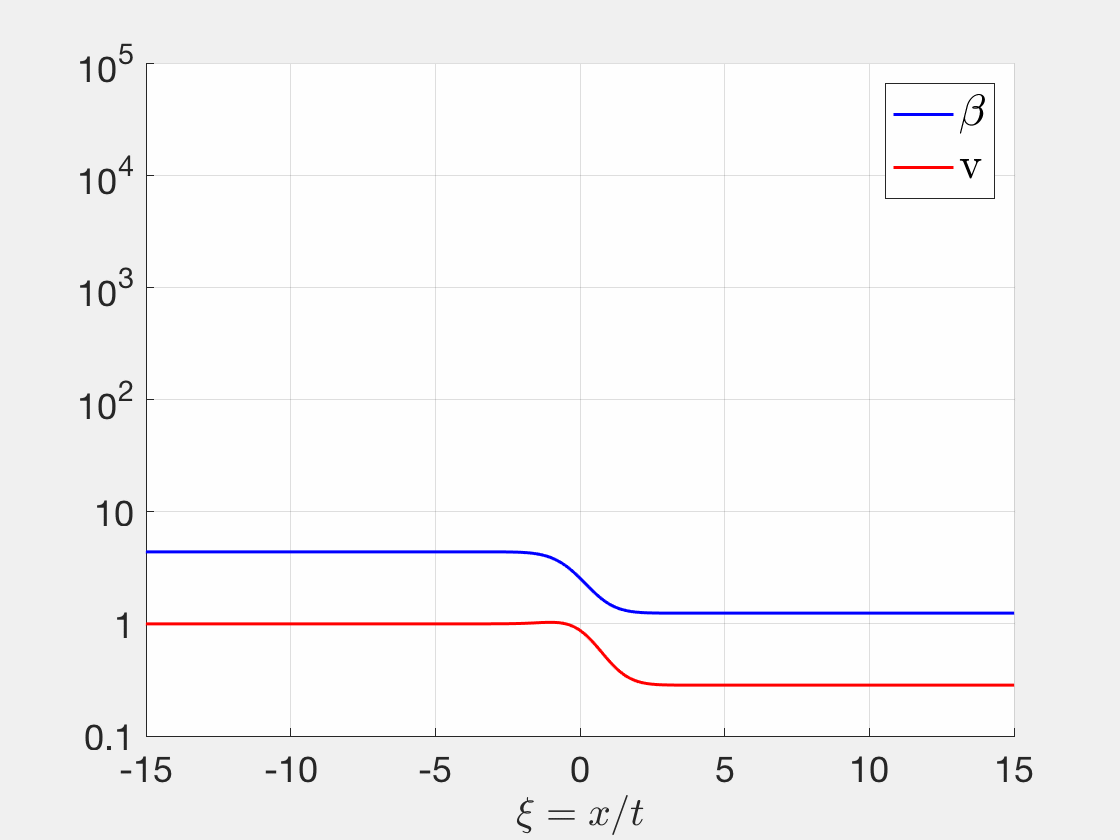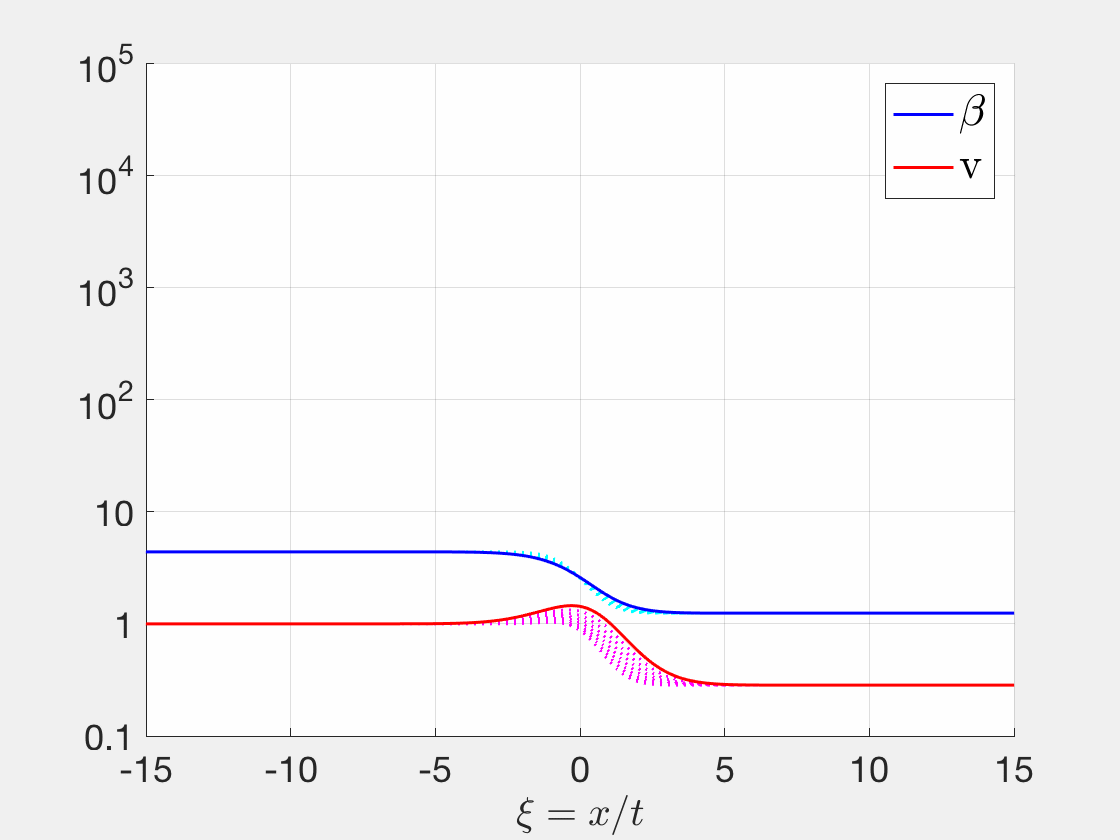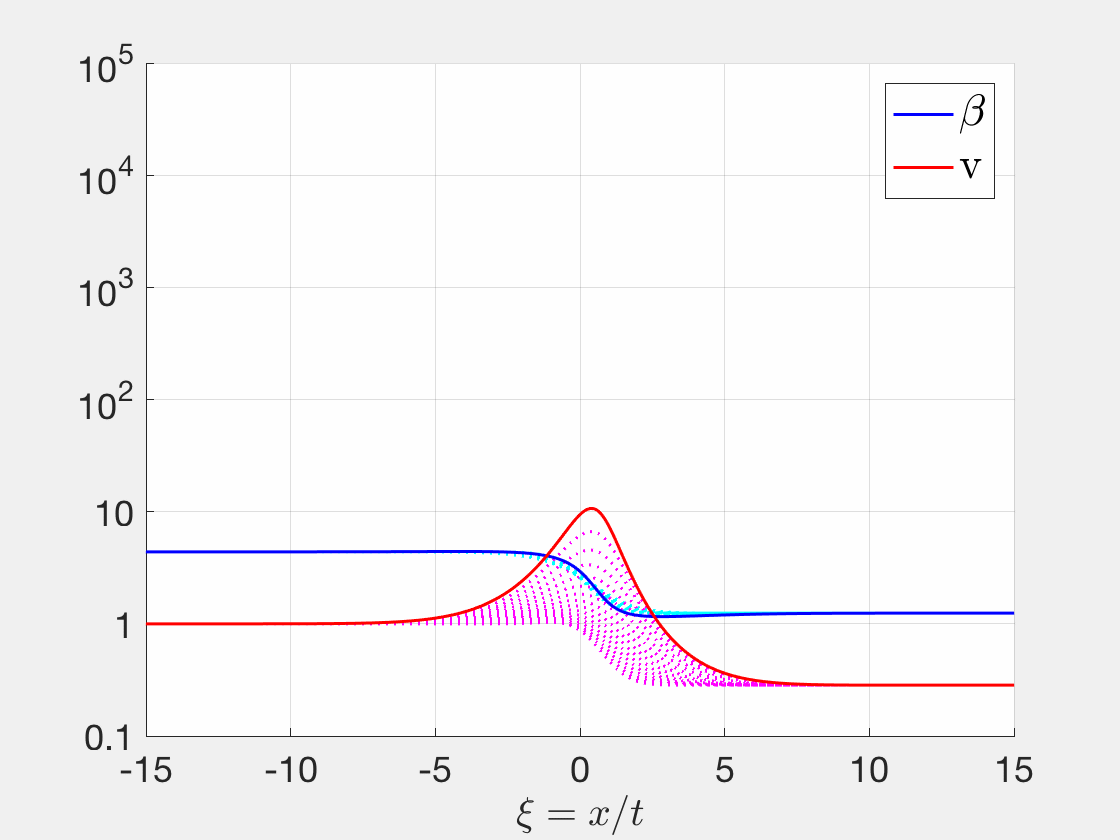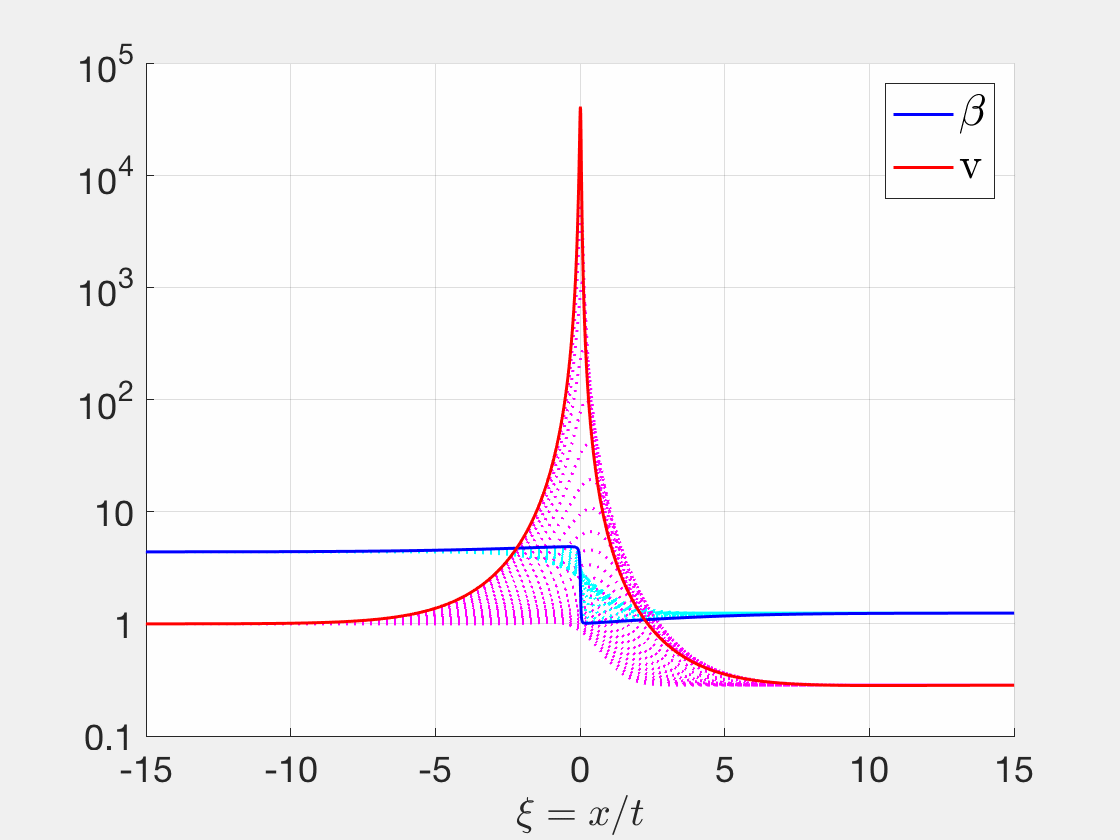
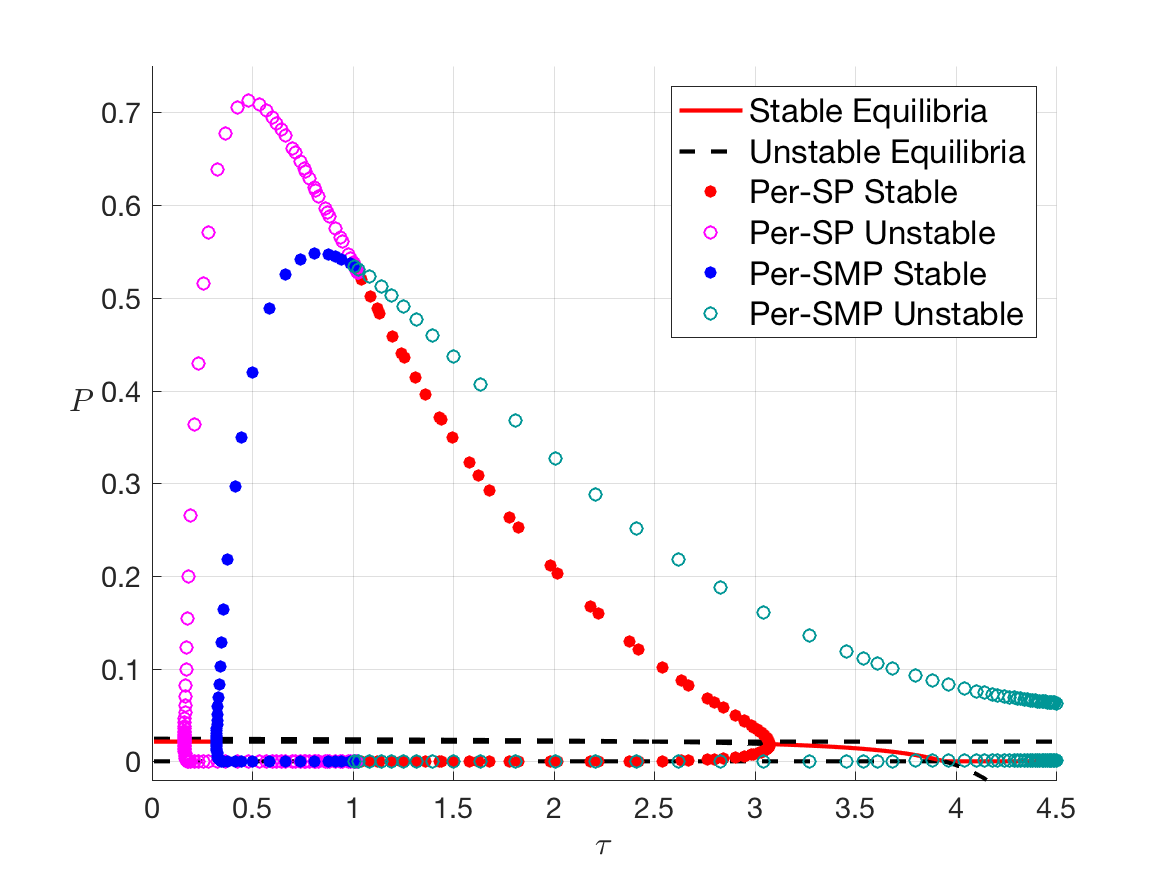
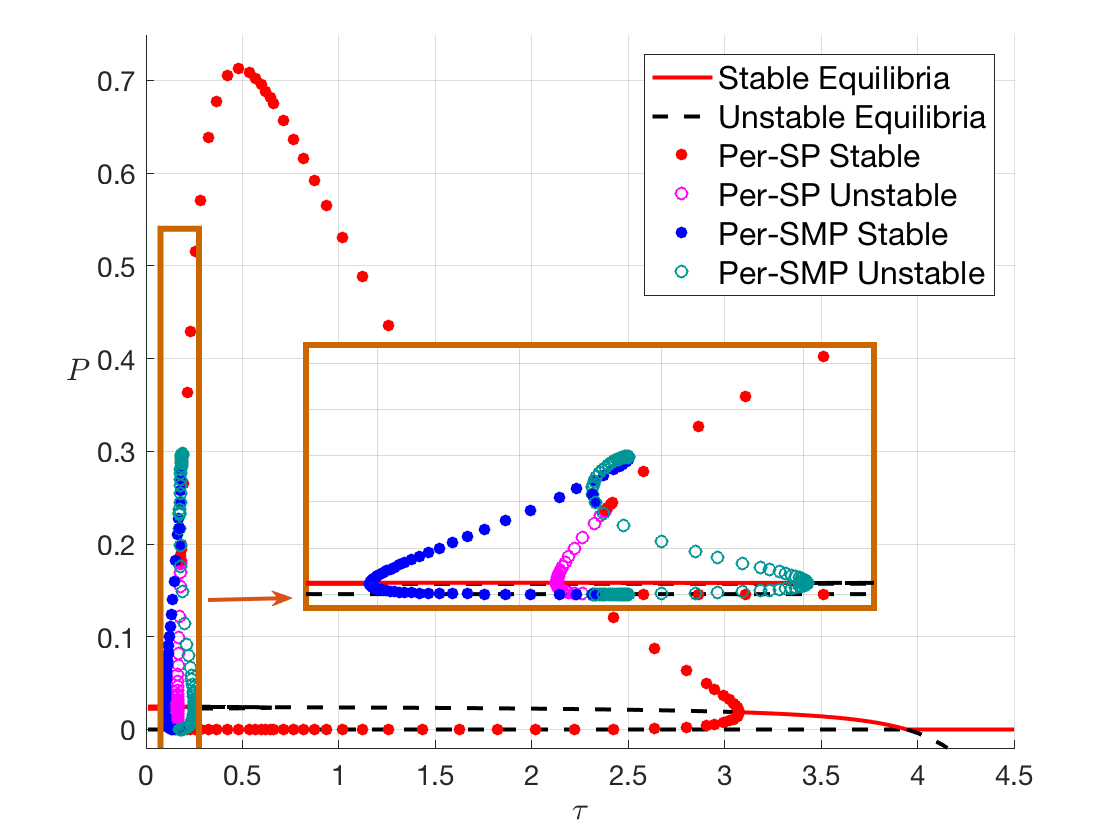
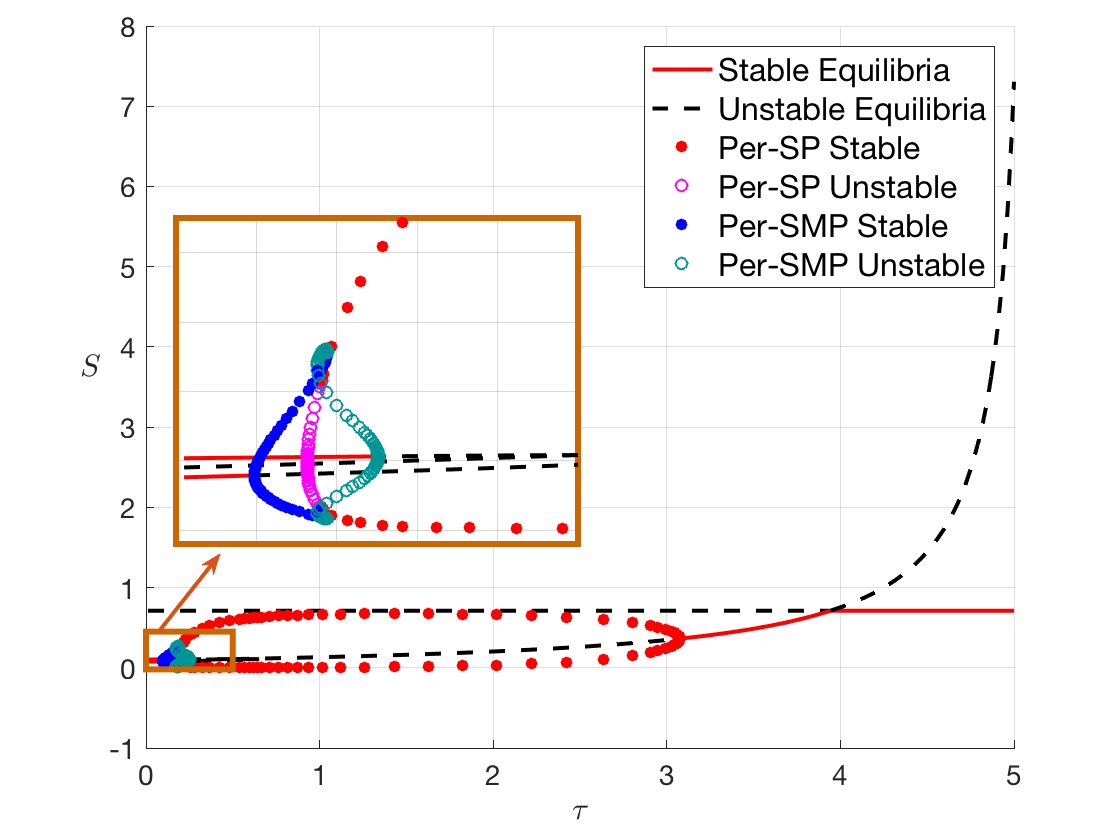
-- Delay Equations for Bacterial Phage

Collaborating with Prof. Wolkowicz, I study delay system modeling the interaction of phage-sensitive and phage-resistant bacteria in a chemostat. Using the software DDE-BIFTOOL for bifurcation analysis, we unveiled some rich dynamics of the system.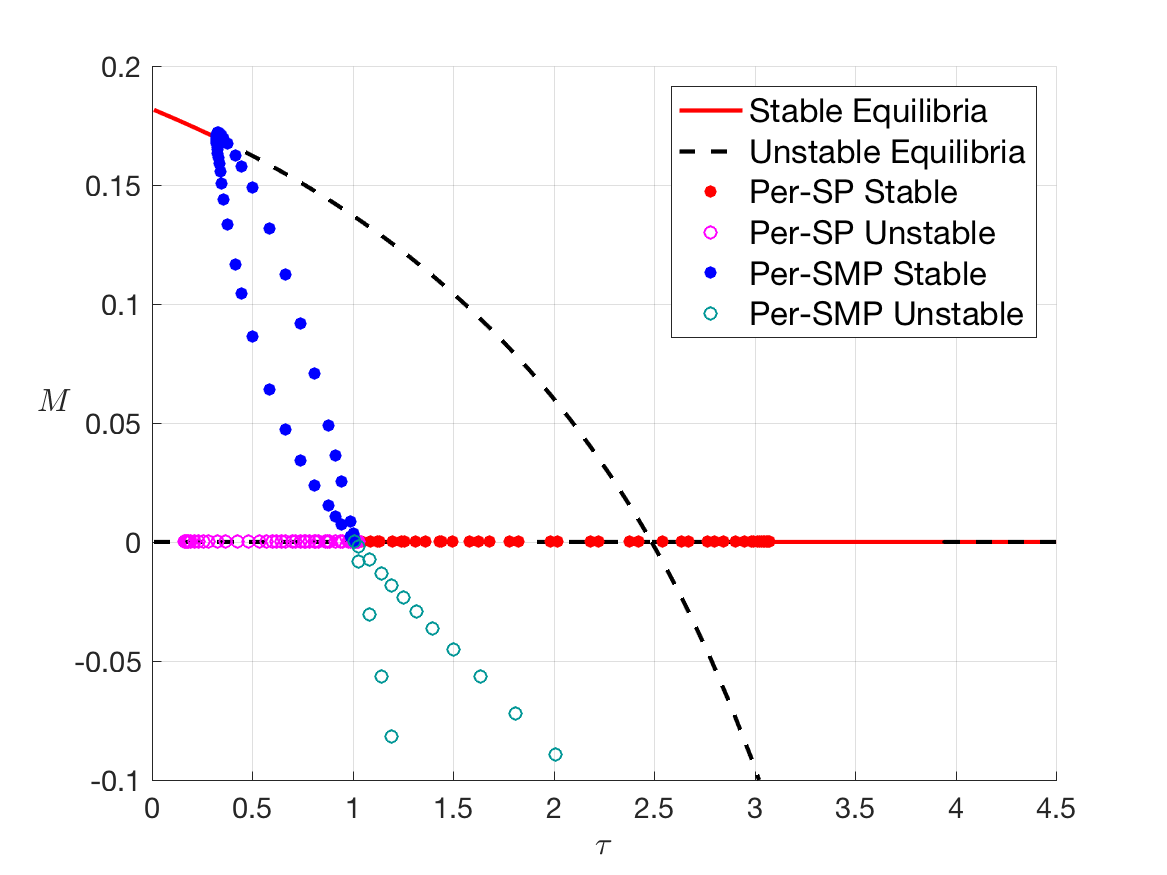

Programing

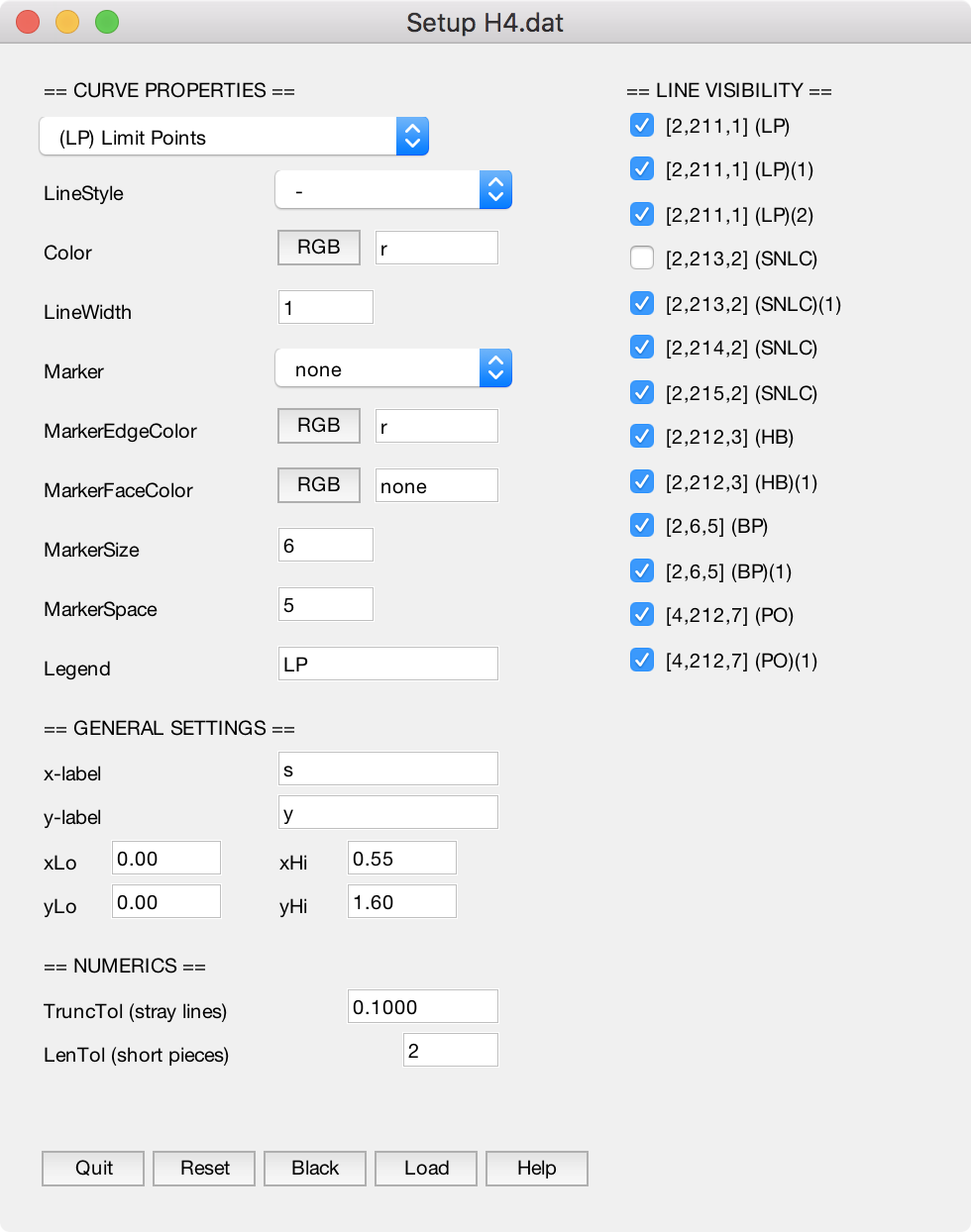
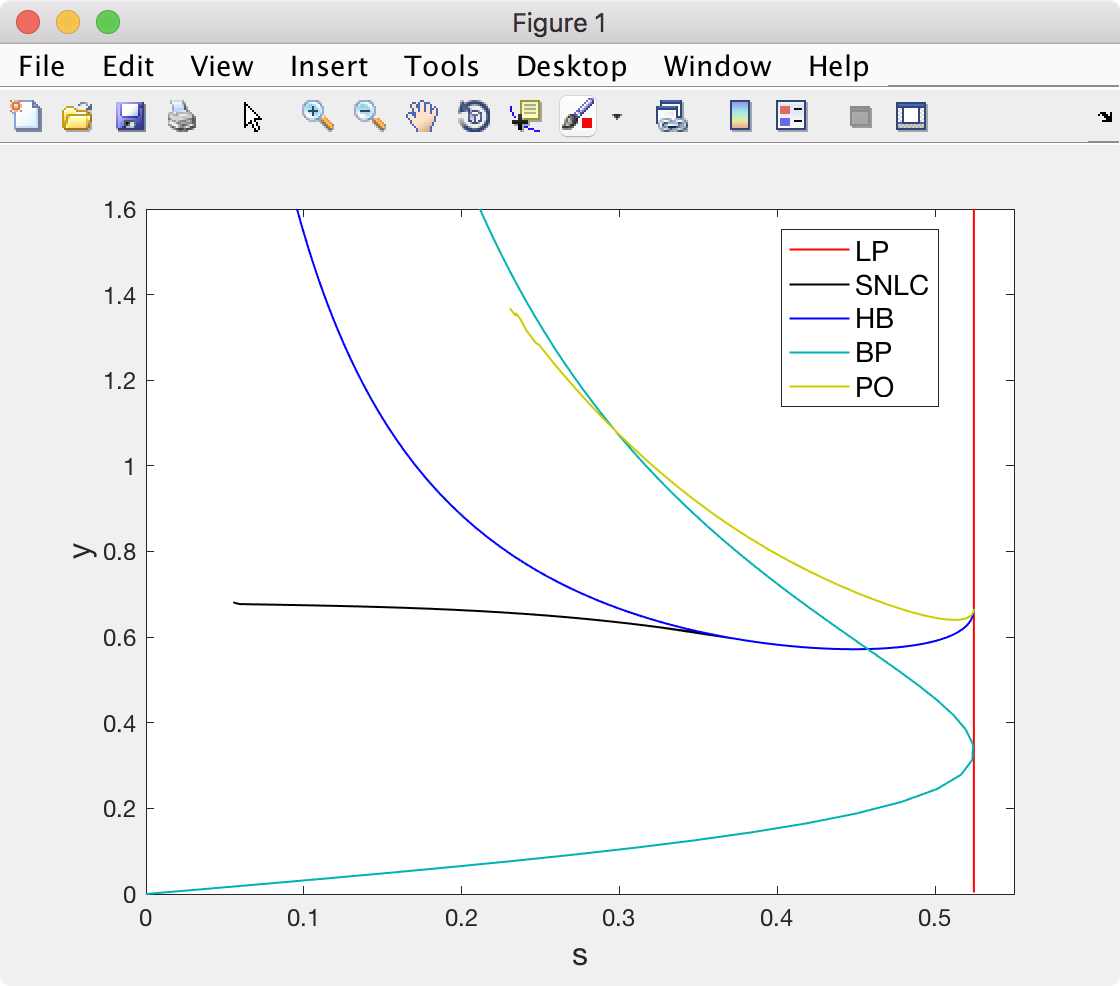
-- MATLAB Script for Plotting Data from XPPAUT

I am proficient in MATLAB programing. In order to produce graphs from data generated by the bifurcation software XPPAUT, I wrote a tool that provides a graphical interface for users to conveniently obtain and customize graphs for the corresponding data. This program has been adopted in the software's official website.